|
SPECIAL NEW CUSTOMER OFFER: Free 30-minute diagnostic session. Limited spots. 415-623-4251.
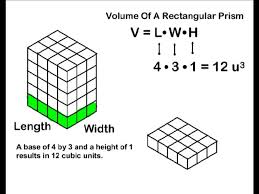
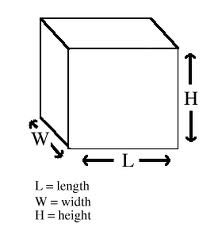
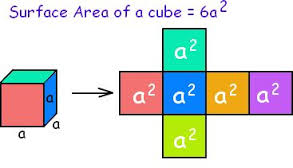
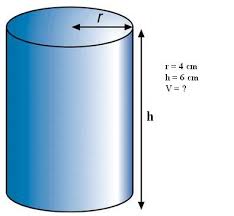
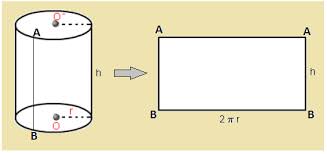
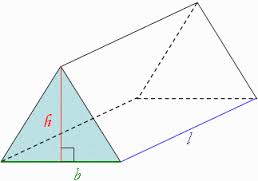
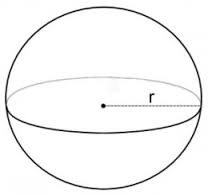
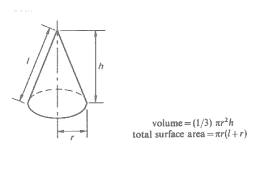
Did you like the TV show “[Br]eaking [Ba]d?” So did I. Follow these tips, inspired by that show, and you won’t be [Sc]oring [Ba]dly on the SAT! Better Call Saul! Know the “law” of the test and how to use it. Any good legal argument is based on authoritative sources, provable evidence, and logic. That means that definitions and authoritative sources are your friends. In the case of a criminal prosecution Saul is defending, the source is the criminal law of New Mexico. In the case of the reading sections, the authoritative source is the passage itself. Read like a meathead literalist. Here’s where knowing something about the subject of a passage can hurt you; you may fall for an answer that is correct, but isn’t mentioned in the passage. The questions will always either ask you what is in the passage, or what can reasonably be inferred from the passage. So don’t pick any answer that isn’t directly stated in the passage, or isn’t an obvious conclusion you can reach by reading the passage. If you have to make too many inferences or assumptions, RUN AWAY! In other words, if you go too far “out on a limb” you will fall off the tree! In the sentence correction questions, the rules of grammar and punctuation are the law; study them! Even if the sentence looks and “sounds” right in your head, is it grammatical? Study the rules in your SAT review book and English textbooks. In the sentence completion questions, use the dictionary definitions of the words, not common slang usages (look words up in the dictionary- you may be surprised as to what they really mean! They often have other meanings than the common one. Don’t believe me? Look up “pervert,” “unique,” “fulsome,” “spastic,” and other words people use, but don’t really understand). Study your Greek and Latin word roots, and you can figure out word meanings. Similarly, on the essay, just remember, you don’t have to argue what you really feel, just what you can “prove” or support with evidence. Like any defense attorney, Saul doesn’t have to prove what he’s saying is true; the prosecutor has to prove it’s false in order to convict Jesse, Walter, or anyone else. Saul can’t help his client if his client talks to the cops, tells them one story, then tells another story on the stand that’s not consistent with the first story. While this isn’t sworn testimony, you want to argue convincingly with relevant and convincing examples. If you can make a better case for the side you don’t agree with, just go with it. It’s not going to be used against you in court ;-) . Rely on diagrams that aren’t marked “Note: Figure Not Drawn to Scale.” You can check the length of lines in diagrams using a “ruler” made of a piece of paper from your test booklet or the side of your answer sheet. Do NOT make unwarranted assumptions. Write out the math or use your calculator if you’re not good at math in your head. Check your work. If you don’t know a common mathematical formula or fact, BETTER CALL SAUL! Look at the “Math Facts” at the beginning of the section. While you should memorize all those facts LONG before the test, if you forget something or are panicking, take a few seconds to go and look. The same goes for use of the calculator- if you know you’re not good at doing arithmetic in your head, or on paper, just use the calculator. Don’t worry about what anyone else is doing. If you don’t know the meaning of a weird symbol (say, a smiley face, a funny-looking cross, or a triangle) used to define a function (mathematical operation), don’t panic! The problem HAS to define it for you. Just read the definition, and I guarantee you’ll know how to do it. “Tread Lightly” – Be Careful and Avoid Drastic Moves. Remember Walter White’s advice to Hank Schrader : “Tread Lightly.” Be careful, but avoid panicking and making drastic moves on test day. “Tread lightly” – don’t pick “sucker punch” answers that are tempting but wrong. (See my entry “Don’t Go to the SPA”). You can avoid that by looking at ALL the answer choices and understanding why the right one is right and the wrong one is wrong. However, don’t worry TOO much about the right answer or the “best” answer. If you overthink your answers, you can end up changing a correct answer to a wrong one, or taking what would have been a great essay and making it a real piece of junk. For example, don’t decide to change your essay completely in the middle of writing it. Take time to think, then set up a little outline in your answer book, which can literally be one or two words on each line. After that, start writing and don’t look back! Don’t contradict yourself by leaving some things in from your first draft, then adding some inconsistent information (unless you can explain the inconsistency). Don’t waste time by starting over again, or by panicking at the beginning. Just pick a position, go with it, write your best argument, and go with it. Similarly, you can psych yourself out with subtle differences in word meanings, or “What do the SAT people *want* me to answer?” Don’t let yourself think “Well, this *could* be right under some circumstances.” The point is to pick the *best* answer, not every *possible* answer. Just read the question, figure out the answer, compare it to the the listed answers, and pick the answer that makes sense to you. The answers will then work to your advantage if you know what the answer should be – just pick the right one. If your answer doesn’t match any of the answers (on a math problem), the SAT people just did you a favor- check your work, re-read the problem, and you’ll get the right answer! Don’t get bogged down in the minute details, and again, don’t make assumptions. Walter White remembered his main purpose – getting money for his family after he was dead. He usually didn’t let extraneous factors get in the way, or make unwarranted assumptions. When he did, it got him in trouble (think about the Los Pollos Hermanos security head). The same applies to you – don’t make assumptions, or you will lose points! On the essay, as stated above, you don’t have to argue your real opinion on a subject, If you can’t figure out how to solve a question within about one minute, pick an answer that seems reasonable and move on. If you can’t see that any of the answers are unreasonable (e.g., it’s a negative number when only a positive one will do), then just SKIP IT, and move on. Even Heisenberg can be certain about this: If you follow this advice, you won’t be scoring badly, and you’ll avoid the blues! SPECIAL NEW CUSTOMER OFFER: Free 30-minute diagnostic session. Limited spots. 415-623-4251. Solid Geometry Rectangular Prisms You will ABSOLUTELY need to know the formula for the volume of a rectangular prism (you know, a box-shaped thing), which is length X width X height. V = L * W * H. Surface Area of a Rectangular Prism: There are three different sets of two rectangular sides – two sides have area L*W; two have area W*H; the last two have area L*H. So SA = 2LW + 2WH +2LH, or 2(LW+WH+LH). Cubes A cube is simply a special case of a rectangular prism – since all the sides, or “edges” are the same length, width, and height, the volume is L * W * H , which is the same as L * L * L, since L=W=H in a cube. So if a cube has edge length 2, the volume is 2 * 2 * 2, which is 2 to the third power (2^3), or “2 cubed.” That’s why the third power of any number is called that number “cubed,” get it? ;-) This information is likely to appear in a word problem where you’re given the volume of the cube and expected to find the edge length (and perhaps find the area of one of the cube’s sides or something else) Surface Area of a Cube: Just take the edge length, square it to find the area of one side, and multiply it by six (a cube has six sides). The surface area is six times the edge length squared. So, SA = e*e*6 or 6e^2. (or 6a^2,as in the figure below). Right Cylinders: The SAT and other tests ask about the volume of a right cylinder (you know, something shaped like a soda can) ALL THE TIME. Count on seeing problems that require you to know the formula for the volume of a cylinder. It’s pretty simple – just take the formula for the area of a circle (good ol’ pi-r-squared) and multiply it by the height. So V = πr^2h, where V is the volume, r is the radius, and h is the height. The surface area of a cylinder is equal to 2(πr^2) + 2πrh. Note on All Solids: Notice that the volume of any 3-dimensional shape (cylinder, prism, etc) is just the area of the end shape, multiplied by the other side (the height, length, or depth – you know, the part that doesn’t form the end shape). So a triangular prism would have a volume of V = 1/2bh*L, where L is the length of the prism, b is the base of the triangle on each end, and h is the height of the triangle. Not that I’ve seen it, but a good SAT problem would be to take a shape formed from two geometric figures, then make it into a prism, so the student has to calculate the area of the shape, then multiply by the length of the other side to get the volume. (Think of a crude version of a hotel or house piece from Monopoly™, where the sides are just squares topped with triangles.) See if you can figure out the formula for the surface are of a triangular prism. Spheres While this is less likely to be on the SAT, it’s worth knowing the formula for the volume of a sphere. The formula for the surface area of a sphere (really not likely to be on the SAT, but here it is): V = (4/3)πr^3 The surface area of a sphere is SA= 4πr^3 Cones
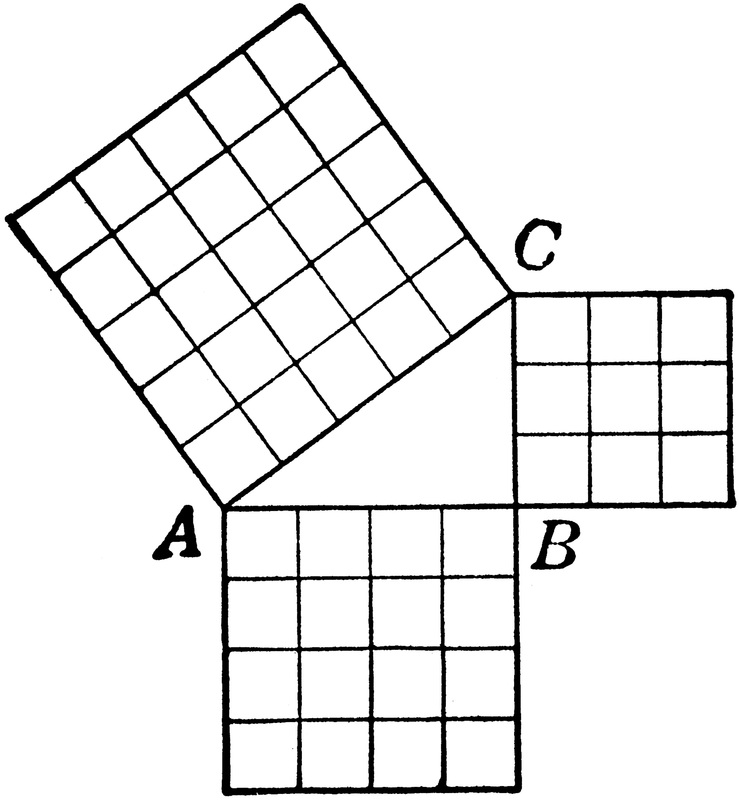
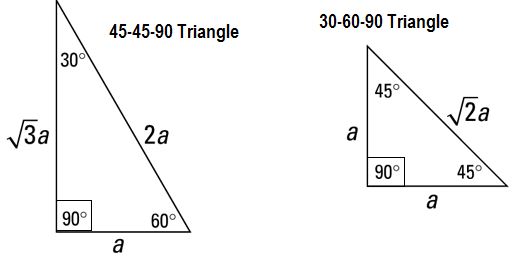
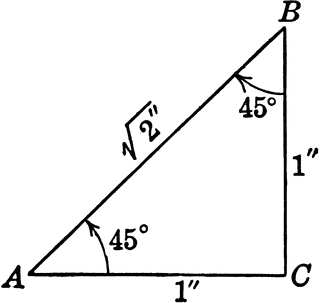
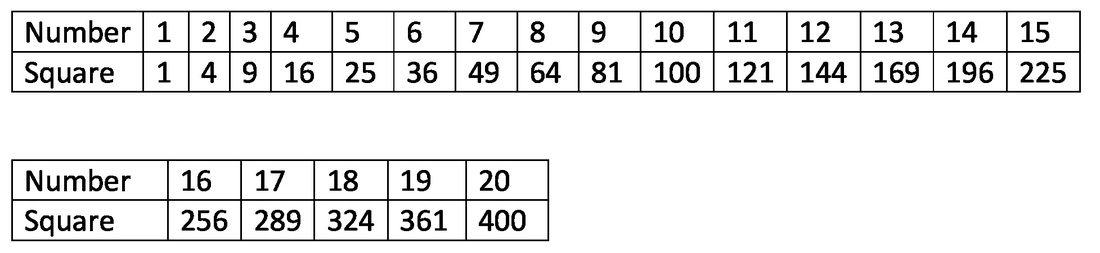
You probably won’t see any questions about cones on the SAT, but just in case: The formula for the volume of a right circular cone is: πr^2(h/3) The formula for the surface area of a right circular cone is: SA = πr(r^2 + √(H^2 + r^2)) Here are some things you should know for the SAT, ACT, GMAT, GRE, or any other standardized test that tests math. Notice that the sides of a triangle can also be the sides of squares, which is something you’re likely to see in an SAT problem. Special Right Triangles 30-60-90 triangle: The ratio of the lengths of the sides opposite the angles are 1,√3, and 2, respectively. That is, the shortest side is 1, the second longest side is √3 hypotenuse is 2. 45-45-90 triangle: The ratio of the lengths of the sides opposite the angles is 1-1-√2. Powers To Remember You should know the powers of 2 from 0 to 10, since powers of 2 are useful for so many SAT problems (e.g., a bacterial culture that doubles the number of cells every period of time). Higher Powers: You really only need to know a few powers higher than 3 on the SAT. You should probably know 1 through 6 to up to the fourth power, and 7 through 9 up to the third power. (To get any power of 10, just add that number of zeroes behind it; 101 = 10, 102 =100, and so on.) Distance Formula: Distance = Rate X Time , so Rate = Distance/Time, Time = Distance For example, 100 miles = 100 miles per hour (miles/hour) * 1 hour. 100 miles/hr = 100 miles/1 hr, and 1 hr = (100 miles)/ (100 miles/ 1hr) = 1 hr. Coordinate Distance formula: As discussed in the Pythagorean Theorem section above, the distance between two points on a Cartesian coordinate (x-y) grid, can be determined using the Pythagorean Theorem and the coordinates. The formula for the distance between points A = (x1, y1) and B = (x2, y2), which we can call AB, is: This formula will help you with coordinate geometry (Cartesian coordinate) problems.
|
Author: John Linneball Who did you think? ;-)I'm the proprietor and only tutor for this business; that's why I named it after me. Archives
June 2024
Categories |

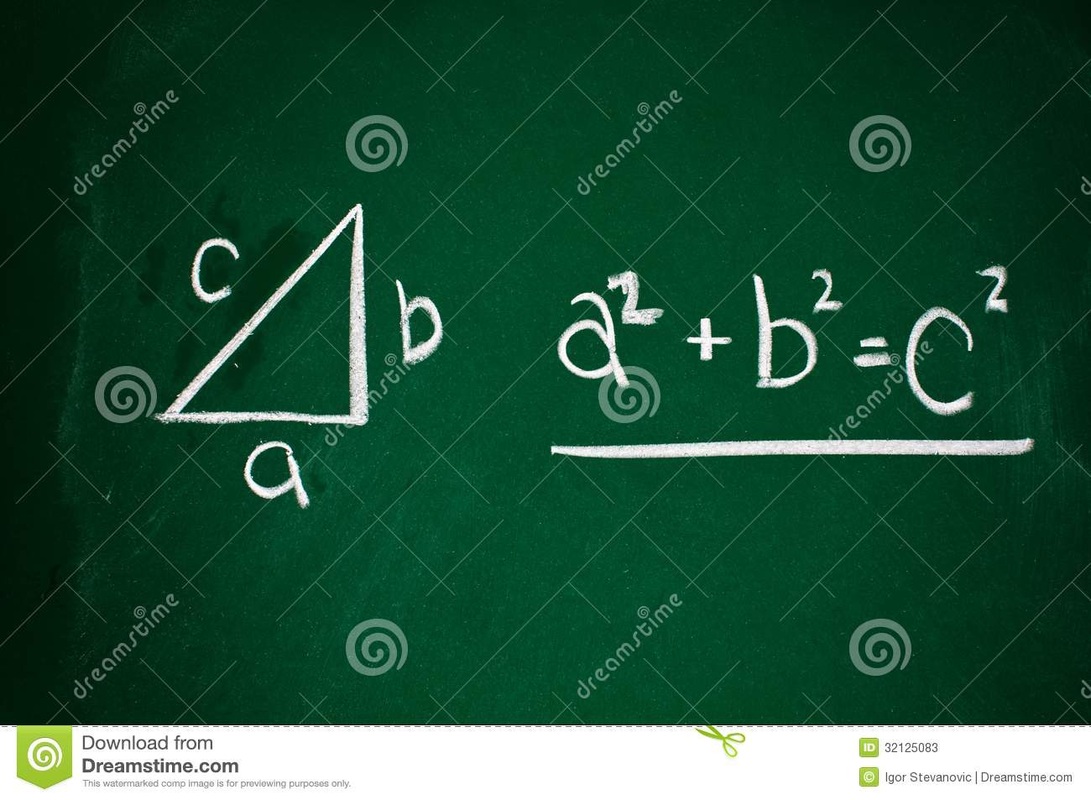

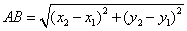
 RSS Feed
RSS Feed