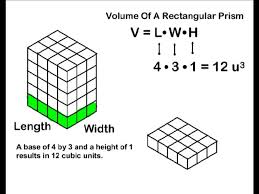
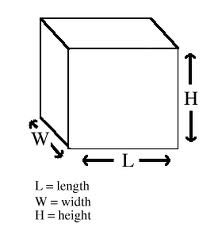
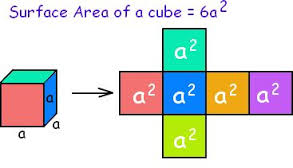
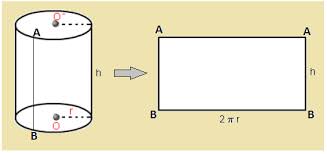
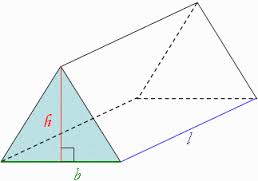
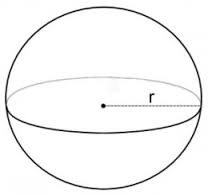
Solid Geometry Formulas for the SAT

Solid Geometry

Rectangular Prisms

You will ABSOLUTELY need to know the formula for the volume of a rectangular prism (you know, a box-shaped thing), which is length X width X height. 

V = L * W * H.  

Surface Area of a Rectangular Prism: There are three different sets of two rectangular sides – two sides have area L*W; two have area W*H; the last two have area L*H.

So SA = 2LW + 2WH +2LH, or 2(LW+WH+LH).

Cubes

A cube is simply a special case of a rectangular prism – since all the sides, or “edges” are the same length, width, and height, the volume is L * W * H , which is the same as L * L * L, since L=W=H in a cube.

So if a cube has edge length 2, the volume is 2 * 2 * 2, which is 2 to the third power (2^3), or “2 cubed.” That’s why the third power of any number is called that number “cubed,” get it? ;-) This information is likely to appear in a word problem where you’re given the volume of the cube and expected to find the edge length (and perhaps find the area of one of the cube’s sides or something else)

Surface Area of a Cube: Just take the edge length, square it to find the area of one side, and multiply it by six (a cube has six sides). The surface area is six times the edge length squared.

So, SA = e*e*6 or 6e^2. (or 6a^2,as in the figure below).

Right Cylinders:

The SAT and other tests ask about the volume of a right cylinder (you know, something shaped like a soda can) ALL THE TIME. Count on seeing problems that require you to know the formula for the volume of a cylinder.  It’s pretty simple – just take the formula for the area of a circle (good ol’ pi-r-squared) and multiply it by the height. So V = πr^2h, where V is the volume, r is the radius, and h is the height.

The surface area of a cylinder is equal to 2(πr^2) + 2πrh.

Note on All Solids:

Notice that the volume of any 3-dimensional shape (cylinder, prism, etc) is just the area of the end shape, multiplied by the other side (the height, length, or depth – you know, the part that doesn’t form the end shape). So a triangular prism would have a volume of V = 1/2bh*L, where L is the length of the prism, b is the base of the triangle on each end, and h is the height of the triangle. Not that I’ve seen it, but a good SAT problem would be to take a shape formed from two geometric figures, then make it into a prism, so the student has to calculate the area of the shape, then multiply by the length of the other side to get the volume. (Think of a crude version of a hotel or house piece from Monopoly™, where the sides are just squares topped with triangles.) See if you can figure out the formula for the surface are of a triangular prism.

Spheres

While this is less likely to be on the SAT, it’s worth knowing the formula for the volume of a sphere.

The formula for the surface area of a sphere (really not likely to be on the SAT, but here it is):

V = (4/3)πr^3

The surface area of a sphere is SA= 4πr^3

Cones

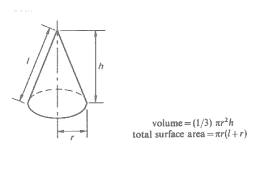
You probably won’t see any questions about cones on the SAT, but just in case:

The formula for the volume of a right circular cone is: πr^2(h/3)

The formula for the surface area of a right circular cone is: SA = πr(r^2 + √(H^2 + r^2))