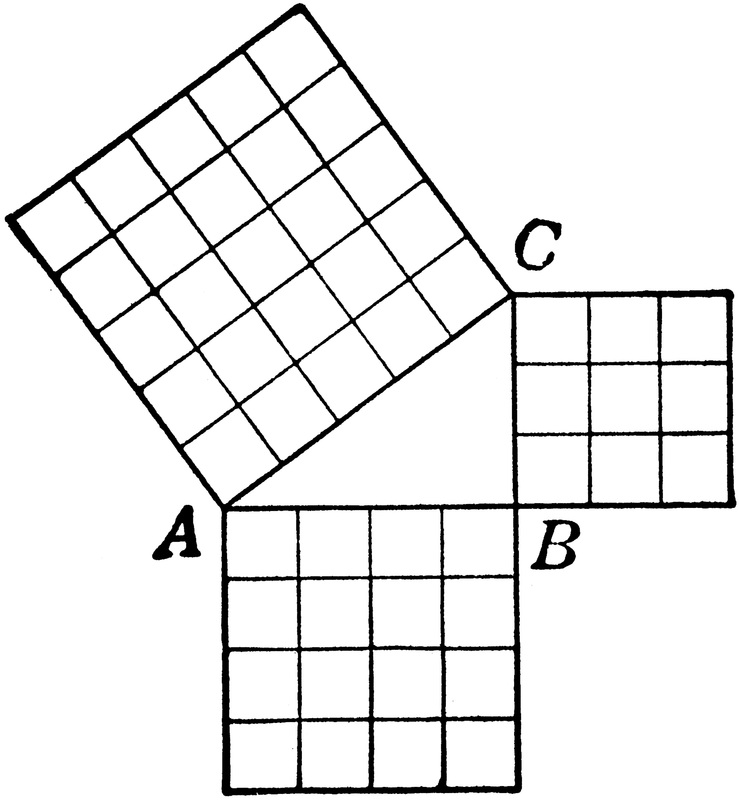
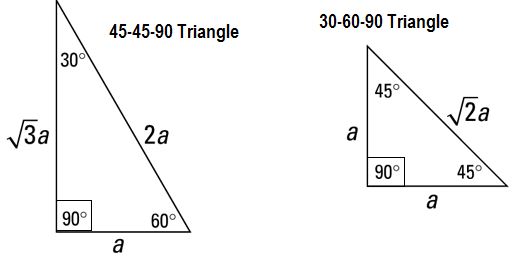
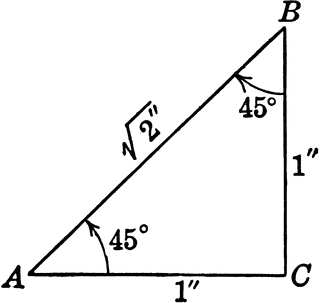
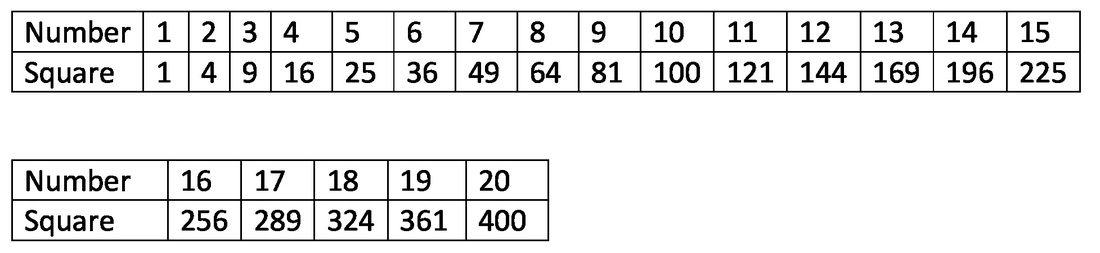
Here are some things you should know for the SAT, ACT, GMAT, GRE, or any other standardized test that tests math. Notice that the sides of a triangle can also be the sides of squares, which is something you’re likely to see in an SAT problem. Special Right Triangles 30-60-90 triangle: The ratio of the lengths of the sides opposite the angles are 1,√3, and 2, respectively. That is, the shortest side is 1, the second longest side is √3 hypotenuse is 2. 45-45-90 triangle: The ratio of the lengths of the sides opposite the angles is 1-1-√2. Powers To Remember You should know the powers of 2 from 0 to 10, since powers of 2 are useful for so many SAT problems (e.g., a bacterial culture that doubles the number of cells every period of time). Higher Powers: You really only need to know a few powers higher than 3 on the SAT. You should probably know 1 through 6 to up to the fourth power, and 7 through 9 up to the third power. (To get any power of 10, just add that number of zeroes behind it; 101 = 10, 102 =100, and so on.) Distance Formula: Distance = Rate X Time , so Rate = Distance/Time, Time = Distance For example, 100 miles = 100 miles per hour (miles/hour) * 1 hour. 100 miles/hr = 100 miles/1 hr, and 1 hr = (100 miles)/ (100 miles/ 1hr) = 1 hr. Coordinate Distance formula: As discussed in the Pythagorean Theorem section above, the distance between two points on a Cartesian coordinate (x-y) grid, can be determined using the Pythagorean Theorem and the coordinates. The formula for the distance between points A = (x1, y1) and B = (x2, y2), which we can call AB, is: This formula will help you with coordinate geometry (Cartesian coordinate) problems.
Your comment will be posted after it is approved.
Leave a Reply. |
Author: John Linneball Who did you think? ;-)I'm the proprietor and only tutor for this business; that's why I named it after me. Archives
June 2024
Categories |
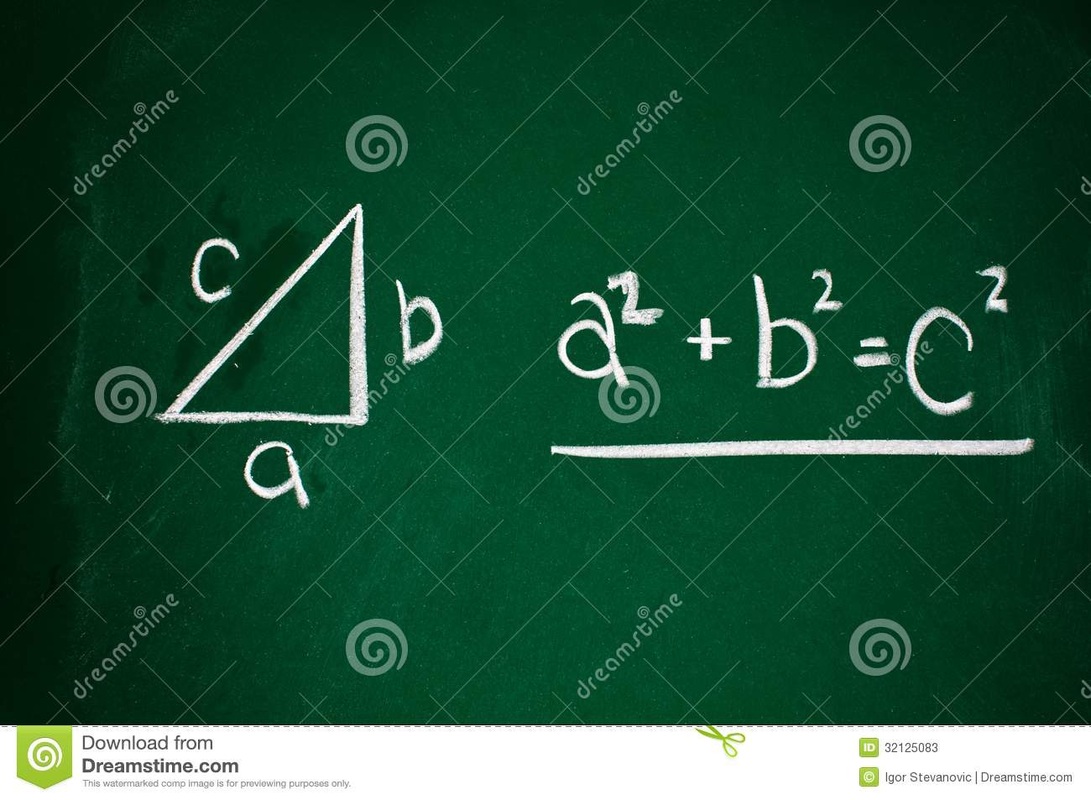

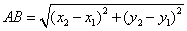
 RSS Feed
RSS Feed