Things to Know for the Math Section of the Upcoming SAT

SPECIAL NEW CUSTOMER OFFER: Free 30-minute diagnostic session. Limited spots. 415-623-4251.

Things to Know for the Math Section of the Upcoming SAT
Here’s a quick list of formulas and other math facts you should know for tomorrow’s SAT. You will have to memorize them; they will not be provided in the “Math Facts” box at the beginning of the math sections.
The “difference of squares”: (a+b)(a-b) = a2 – b2
Other binomials:
(a+b) = a2 +2ab + b2
(a-b) = a2 - 2ab + b2
 
The Relationship of the Diagonal of a Square to its Area.
A = d2/2. This comes from the fact that a square’s diagonal splits it into two 45-45-90 triangles, which have the side ratio of 1-1-√2, so the side length, s, is equal to d/√2, and the area, which is s2, is then equal to (d/√2)2, which is d2/2.
Know that a square’s diagonals bisect, are congruent (equal), and are perpendicular, to each other.
Important Properties of Parallelograms:

1. Angles that are diagonal to each other are equal.
2. Consecutive angles (ones that are next to each other) are supplementary (they add up to 180 degrees).
3. If one angle is a 90-degree (right) angle, then they all are.
4. The diagonals bisect each other.
5. Each diagonal bisects the parallelogram into two congruent triangles.

Note that rectangles and squares are also parallelograms, so these properties also apply to rectangles and squares. The diagonals of squares are also perpendicular (they form 90-degree angles).
 
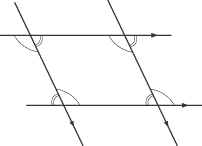
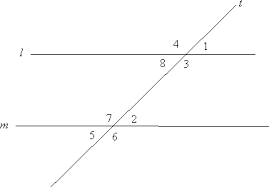
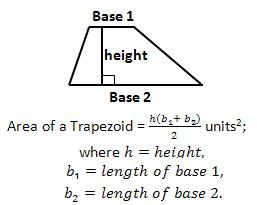
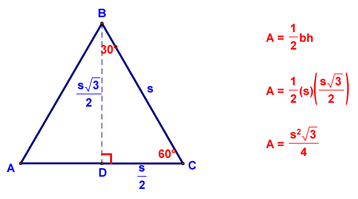
Properties of transversals (two pairs parallel lines that cross each other).

​Notice that parallelograms are formed by transversals (two pairs of parallel lines).

Notice that angle 1 = angle 8 = angle 2 =angle 5 and angle 4=3=7=6. If there were a line parallel to line t, the corresponding angles formed with line l and m would also be equal (congruent) to the angles line t formed with lines l and m (that is, all the acute angles are congruent, and all the obtuse angles are congruent). See the first diagram in this section. Obviously, if they were all right angles, all the angles would be congruent, since they’d all be 90 degrees.

Area of a Trapezoid:

How to Find the Area of an Equilateral Triangle if All You Know is the Side Length:

Here, if you know the side length is s, then you know you can split the triangle into two 30-60-90 triangles with side lengths s/2, s, and s√3. The s√3. side is the altitude of the triangle that splits it in two. So the area of one 30-60-90 triangle is 1/2 * s√3. * s/2, and the area of the whole equilateral triangle is (s*s√3)/4, which is (s2√3)/4. You can memorize this formula, or just know how to derive it by using an altitude to split the triangle in two.

I hope these formulas and facts help. Please read my other blog entries for other tips. Good luck on the SAT!

​SPECIAL NEW CUSTOMER OFFER: Free 30-minute diagnostic session. Limited spots. 415-623-4251.